Top voor de ATT

Afgelopen juli was ik nog druk aan het werk om mijn top te quilten voor de Algemene tentoonstelling. Ik quilt meestal met de hand. Maar deze top is best wel groot en op de hand quilten zou me nog wel een jaar of wat kosten. Daarom besloot ik om deze top op de naaimachine te quilten. Ik was gewoon lekker voor me uit een beetje aan het quilten op mijn naaimachine, de naden aan het doorstikken. Tot ik bij een blok kwam waarbij ik even de quiltweg kwijt raakte. Hoe kon ik dit blok zo quilten, dat ik elke naad maar 1 keer naaide en dat ik niet hoefde af te hechten?

Ik probeerde het een keer op papier, maar daar had ik geen geduld voor. Ik ging er maar gewoon voor. Maar ik moest wel drie keer aan- en afhechten voordat het mij lukte om alle naden van het blok te quilten. Nu heb ik weinig ervaring met quilten op de naaimachine. Dus het kan zijn dat mijn verhaal over een Euler pad allang bij jullie bekend is en/of op een handiger manier op te lossen is. Maar dit is mijn verhaal.

Euler pad

Mijn partner is wiskundige en het leek me voor hem een leuke uitdaging om dit eens op te lossen. Hoe kun je dit blok nou quilten met als eisen dat er maar 1 keer aan- en afgehecht mag worden en dat elke naad precies 1 keer gestikt wordt? Hij krabde even op zijn hoofd en vroeg toen: “een Euler pad dus”? Nu had ik daar nog nooit van gehoord, maar het leek me in ieder geval leuk dat dit probleem een naam had.

Ik heb het even opgezocht op internet. Daar vind je op wikipedia de volgende tekst:

De wiskundige Leonhard Euler heeft zich onder meer beziggehouden met het probleem van de zeven bruggen van Koningsbergen. Dit probleem komt neer op de vraag of het mogelijk is in een samenhangende graaf, zoals bij de zeven bruggen, een wandeling te vinden waarin alle zijden één keer voorkomen. Zo’n wandeling heet een eulerwandeling. Het is ook de vraag dat een dergelijke wandeling bestaat zodat deze begint en eindigt in dezelfde knoop, dat heet een eulercykel.

Precies wat ik zocht dus! En als de “wandeling” op mijn quilt nu ook nog eens op hetzelfde punt uitkomt als waar het begint, dan kan ik zonder aan- en af te hechten twee van die blokken quilten!

Maar voordat mijn partner aan een oplossing kon werken, moesten eerst de “knopen” geteld worden. Een knoop is een punt waar de lijnen, in dit geval dus de naden, samenkomen. Er is alleen maar een oplossing als het aantal lijnen bij iedere knoop even is. Er mag geen “knoop” zijn waarbij het aantal naden oneven is, maar er is een uitzondering: er mogen er wel precies 2 zijn met het aantal naden oneven. En in zo’n knoop waar een oneven aantal lijnen samenkomt, moet je de wandeling dan wel beginnen en eindigen.

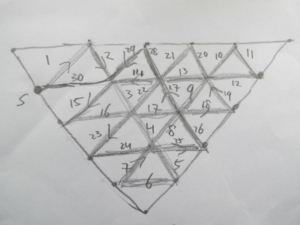
Dus tellen maar…. Gelukkig bleek dit geen probleem te zijn, allemaal even “knopen”. Hieronder het pad zoals mijn vriend dat voor mij uitgetekend heeft. Ik volgde de aangegeven lijnen van 1 naar 30 en het werkte perfect!

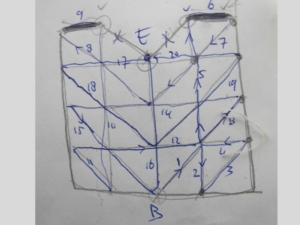
Ik had nog zo’n blok, in de hoeken, en daar kon gelukkig ook een Euler pad voor gemaakt worden. Bij de punten B (van Begin) en E (van Eind) zijn er 5 naden, dus in deze punten moet je beginnen dan wel eindigen.

Dit is het eindresultaat. De foto is gemaakt door onze fotograaf, Harry Roelands. Het ontwerp is gebaseerd op de Bathwick quilt van Karen Styles. Ik heb hier en daar wat weggelaten en wat extra applicaties en borduursel toegevoegd.

Kleedje voor de kat

En hoe zit het nou met dat kleedje voor de kat?

Na het maken van mijn quilt had ik nog allerlei restjes over. Ik heb daar voor de kat een leuk kleedje van gemaakt (zonder Euler pad). En het wordt op prijs gesteld door mevrouw ….